You're backing a bet and its odds are moving - how low can they go while still making a profit?

Someone you follow, whom you know to be an excellent punter, tweets a bet that looks simply too good to be true. So you quickly go to SomeRandomBookmaker.com, only to be annoyed by finding that the odds have moved in the wrong direction. And you were only a minute late! So now you're left wondering: are the odds still playable?

Does this sound like a familiar scenario? Well, today we'll be looking at how to calculate whether the odds are still fine, and also at some traps to think about in addition to the odds. In order for this to work, we need to know the punter's ROI, for a simple reason: the ROI is a mathematical metric of how good a punter is, and math is obviously what we need to calculate the odds.

Trap 1: ROI isn't perfect. The punter needs several hundred bets at the very least for their ROI to be somewhat reliable. And even then, there are related problems: those bets really need to be locked to be trustworthy, and the punter may be great at one market but shite at another. Do be careful. If you do not know the punter's ROI, or just go blindly by what they claim on Twitter - then we strongly suggest you do not back them anyway.

We're proud to be fully transparent on ThePlayer.com: all of our expert tipsters place their bets with legitimate bookmakers, locked in advance, in publically available spreadsheets.

And for those of you who just want the formula - it is dead simple! This way: shared odds / ROI = lowest playable odds. We'll spend the rest of the guide going through why this is the case.

(Note that as we're making calculations using percentages, we'll use decimal odds below greatly simplify our equations. If you're new to decimal odds, they simply state how much is returned on a winning bet. So if you bet £10 on odds of 3.25 and you win, you get £32.5 back for £22.5 in profits.)

An example

Let's start at the very beginning with a punter who has a return on investment (ROI) of exactly ±0. In other words: we expect a bet from this person to go breakeven in the long run.

Let's also say that we have odds of 2.00 - evens - since that means a 50 % chance of winning and is hence simple to calculate.

In this scenario, it should be obvious that if the odds decrease after the bet was shared, it is not worth your attention. And if it increases again, then it is worth it.

Trap 2: Odds can move for a wide variety of reasons, and pinpointing the exact one can be dreadfully difficult. If a punter specialising in a small market shares a great bet, it may very well lead to the whole market moving - but in a different scenario, a punter may have reacted quickly to a recently published injury report, profiting from new information on a bet that would have been neglected otherwise.

The maths

The basic principle is simple. ROI is a measure in per cent of how much better a bet is in reality than in a bookmaker's evaluation of it. This is true regardless of what the odds are, since per cent is a relative measurement. So if our hypothetical punter has a +5% ROI, what this means is that each bet the punter places is valued 5 % higher in terms of probability than the odds given to it by the bookmaker.

Since the odds are just another way of expressing probability, what we want is to:

1. Convert the odds to a probability by takeing 1 / odds = probability
2. Take the positive ROI of the punter and add that to the probability of the bet - since we know that the punter does a few percent better than the odds.
3. Convert this summed probability back to breakeven odds, using the same calculation but in reverse: 1 / probability = odds

Let's take that +5% ROI again, with 2.00 odds, then we know that the punter has 5% positive ROI to add to the odds. And since 1 / odds = probability, we know that the probability is 50 %, since 1 / 2.00 = 0.5

Trap 3: Do note that we can't just add 50 + 5 = 55%. This is because we're adding 5 % of the probability - not of the odds. It's easy to see why. Let's say the odds are 1.04 and we're supposed to add 5 %. That gives us these three steps:

1. Odds to probability: 1 / 1.04 = 0.962 = 96.2%
2. Adding 5 %: 96.2 + 5 = 101.2%
3. Probability back to odds: 1 / 101.2% = 1 / 1.012 = 0.988

In other words, we just calculated that placing bets at lower odds than your money back is profitable! We'll just assume that everybody understands why this is a horrible idea.

Instead, we start with 50 %, and add those 5 % only in step two. Like this: 50 + (50 * 0.05) = 50 + 2.5 = 52.5%. A simpler way of calculating is just taking 50 * 1.05, where we use the ROI directly - it ends up the same anyway.

Then we convert back: 1 / 52.5% = 1 / 0.525 = 1.905. We now know that the evaluation is profitable at about 1.905, when it approaches breakeven.

Put simpler

As mentioned at the top, it's possible to do this in a much easier way. Since odds and probability are just two ways of expressing the same thing, we can just skip the conversion steps, grabbing those extra per cents directly from the ROI instead. The only difference is that we now remove from the odds instead of adding to the probability - since odds and probability are each other's inverses.

Hence, we now use division instead of multiplication, leaving us with 2.00 / 105% = 2.00 / 1.05 = 1.905 again - much easier to get a quick result. Anyone with a calculator and third grade maths knowledge can do it in five seconds.

In conclusion

Just for fun, we simulated 100,000 bets with an ROI of +6.5%, at odds of 1.72, with the lowest playable odds hence being 1.72 / 1.065 = 1.615. Betting one unit per bet gives us this graph:

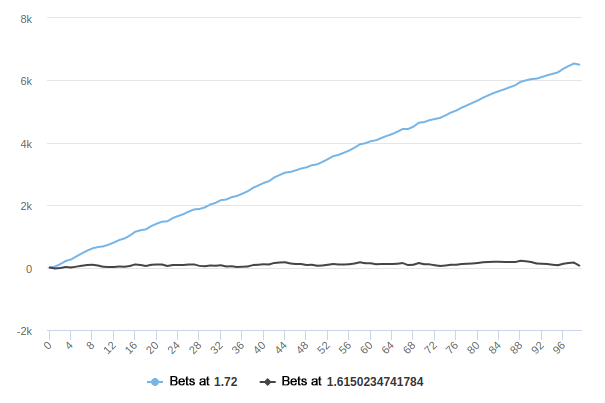
The x axis is the number of bets in thousands, and the y axis is our winnings in units. We also simulated a billion bets, which gave us two practically straight lines in this scale - completely correct but looking somewhat boring.

However, this brings us to our last trap:

Trap 4: Note how close the smaller odds are to breakeven. That those bets ended up with small winnings is completely arbitrary - it could just has well have made a loss. But it illustrates the point well: backing a bet at the lowest playable odds isn't necessarily a good idea. There's no point in betting just above the breakeven point, since the uncertainty is simply too large. After all: we cannot recommend backing punters with ROI in the low single decimals, unless they have a few thousand logged bets and we know that they're good at what they do. The risk is just too large.

So given this example, with 1.72 odds and +6.5% ROI, this author would join in on the action down to around 1.65-1.68 or so, depending on the risk. But, as always, what you end up choosing is of course completely up to you.